문제
3×N 크기의 벽을 2×1, 1×2 크기의 타일로 채우는 경우의 수를 구해보자.
입력
첫째 줄에 N(1 ≤ N ≤ 30)이 주어진다.
출력
첫째 줄에 경우의 수를 출력한다.
힌트
아래 그림은 3×12 벽을 타일로 채운 예시이다.
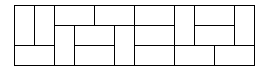
풀이


2만큼의 길이에 타일을 배열하는 경우의 수는 3가지이고, 2를 제외한 2의 배수만큼의 길이에 타일을 배열하는 경우의 수는 왼쪽처럼 2가지다. 우선 4의 길이에서 중간 블럭이 상, 하 블럭 중 하나와 어긋나게 배열되면 나머지 블럭들이 어떻게 배열되는지 정해지며, 어긋나는 부분이 위쪽이냐 아래쪽이냐에 따라서 경우가 정해지므로 2가지다.
길이가 6, 8, 10 ....인 경우에는 왼쪽 패턴이 몇번 반복되냐의 문제라서 2가지로 동일하다.
n = int(input())
dp = [0] * (n+1)
# 2 + dp[2] * 2 + .... + dp[i-4] * 2 + dp[i-2] * 3 = dp[i]
# 입력 값이 홀수일때 배열할 수 있는 경우는 존재하지 않음
if n % 2 == 1:
print(0)
else:
dp[2] = 3
# bottom up, 2칸씩 간격
for i in range(4,n+1,2):
dp[i] = dp[i-2] * 3 + 2 * sum(dp[:i-3]) + 2
print(dp[n])'Python3 알고리즘' 카테고리의 다른 글
| [Python] [백준🥇4] 26008번 해시 해킹 (0) | 2023.03.18 |
|---|---|
| [Python] [백준🥉3] 10818번 최소, 최대 (List) (0) | 2023.03.16 |
| [Python] [백준🥈3] 1021번 회전하는 큐 (Queue) (0) | 2023.03.14 |
| [Python] [백준🥇5] 25556번 포스택 (스택 자료구조) (0) | 2023.03.13 |
| [Python] [백준🥈1] 2178번 미로 탐색 (BFS 알고리즘) (0) | 2023.03.12 |